Overview#
abess (Adaptive BEst Subset Selection) library aims to solve general best subset selection, i.e.,
find a small subset of predictors such that the resulting model is expected to have the highest accuracy.
The selection for best subset shows great value in scientific researches and practical applications.
For example, clinicians want to know whether a patient is healthy or not
based on the expression level of a few of important genes.
This library implements a generic algorithm framework to find the optimal solution in an extremely fast way 1. This framework now supports the detection of best subset under: linear regression, (multi-class) classification, censored-response modeling 2, multi-response modeling (a.k.a. multi-tasks learning), etc. It also supports the variants of best subset selection like group best subset selection 3 and nuisance best subset selection 4. Especially, the time complexity of (group) best subset selection for linear regression is certifiably polynomial 1 3.
Quick start#
The abess software has both Python and R's interfaces. Here a quick start will be given and
for more details, please view: Installation.
Python package#
Install the stable abess Python package from PyPI:
$ pip install abess
or conda-forge
$ conda install abess
Best subset selection for linear regression on a simulated dataset in Python:
from abess.linear import abessLm
from abess.datasets import make_glm_data
sim_dat = make_glm_data(n = 300, p = 1000, k = 10, family = "gaussian")
model = abessLm()
model.fit(sim_dat.x, sim_dat.y)
See more examples analyzed with Python in the Python tutorials.
R package#
Install abess from R CRAN by running the following command in R:
install.packages("abess")
Best subset selection for linear regression on a simulated dataset in R:
library(abess)
sim_dat <- generate.data(n = 300, p = 1000)
abess(x = sim_dat[["x"]], y = sim_dat[["y"]])
See more examples analyzed with R in the R tutorials.
Runtime Performance#
To show the power of abess in computation,
we assess its timings of the CPU execution (seconds) on synthetic datasets, and compare them to
state-of-the-art variable selection methods.
The variable selection and estimation results as well as the details of settings are deferred to Python performance
and R performance. All computations are conducted on a Ubuntu platform with Intel(R) Core(TM) i9-9940X CPU @ 3.30GHz and 48 RAM.
Python package#
We compare abess Python package with scikit-learn on linear regression and logistic regression.
Results are presented in the below figure:
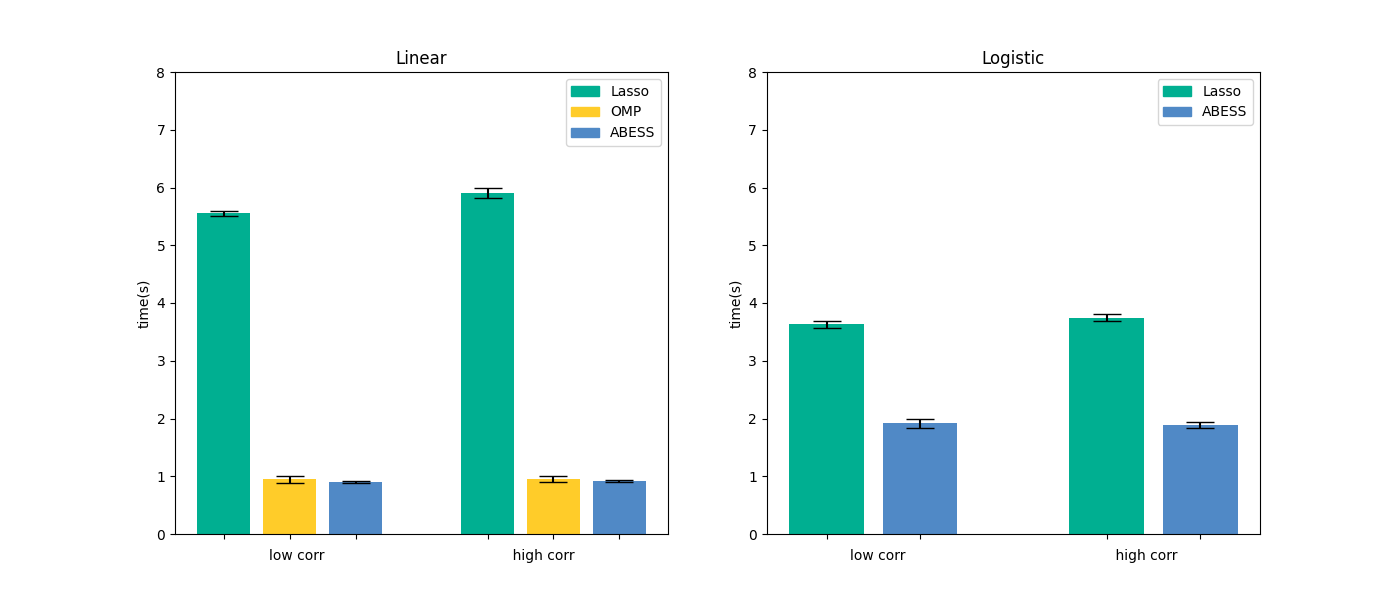
It can be seen that abess uses the least runtime to find the solution. The results can be reproduced by running the commands in shell:
$ python ./docs/simulation/Python/timings.py
R package#
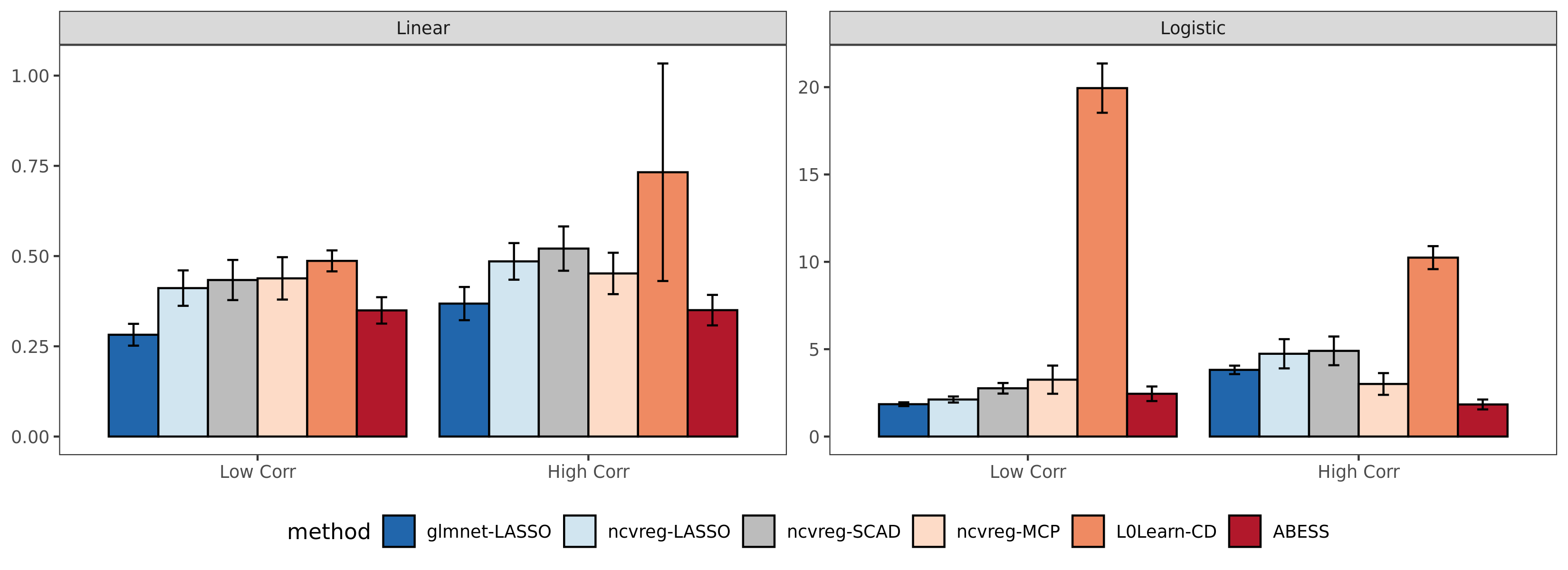
We compare abess R package with three widely used R packages: glmnet, ncvreg, and L0Learn.
We get the runtime comparison result:
Compared with the other packages,
abess shows competitive computational efficiency, and achieves the best computational power when variables have a large correlation.
Conducting the following commands in shell can reproduce the above results:
$ Rscript ./docs/simulation/R/timings.R
Open source software#
abess is a free software and its source code is publicly available in Github.
The core framework is programmed in C++, and user-friendly R and Python interfaces are offered.
You can redistribute it and/or modify it under the terms of the GPL-v3 License.
We welcome contributions for abess, especially stretching abess to
the other best subset selection problems.
What's new#
Citation#
If you use abess or reference our tutorials in a presentation or publication, we would appreciate citations of our library 5.
The corresponding BibteX entry:
@article{JMLR:v23:21-1060,
author = {Jin Zhu and Xueqin Wang and Liyuan Hu and Junhao Huang and Kangkang Jiang and Yanhang Zhang and Shiyun Lin and Junxian Zhu},
title = {abess: A Fast Best-Subset Selection Library in Python and R},
journal = {Journal of Machine Learning Research},
year = {2022},
volume = {23},
number = {202},
pages = {1--7},
url = {http://jmlr.org/papers/v23/21-1060.html}
}
References#
- 1(1,2)
Junxian Zhu, Canhong Wen, Jin Zhu, Heping Zhang, and Xueqin Wang (2020). A polynomial algorithm for best-subset selection problem. Proceedings of the National Academy of Sciences, 117(52):33117-33123.
- 2
Pölsterl, S (2020). scikit-survival: A Library for Time-to-Event Analysis Built on Top of scikit-learn. J. Mach. Learn. Res., 21(212), 1-6.
- 3(1,2)
Yanhang Zhang, Junxian Zhu, Jin Zhu, and Xueqin Wang (2022). A Splicing Approach to Best Subset of Groups Selection. INFORMS Journal on Computing (Accepted). doi:10.1287/ijoc.2022.1241.
- 4
Qiang Sun and Heping Zhang (2020). Targeted Inference Involving High-Dimensional Data Using Nuisance Penalized Regression, Journal of the American Statistical Association, DOI: 10.1080/01621459.2020.1737079.
- 5
Zhu Jin, Xueqin Wang, Liyuan Hu, Junhao Huang, Kangkang Jiang, Yanhang Zhang, Shiyun Lin, and Junxian Zhu. "abess: A Fast Best-Subset Selection Library in Python and R." Journal of Machine Learning Research 23, no. 202 (2022): 1-7.
USING ABESS