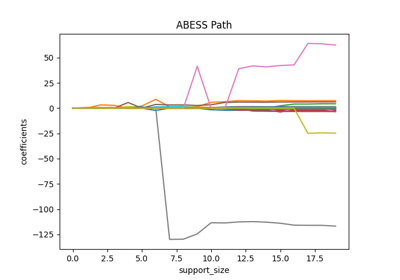
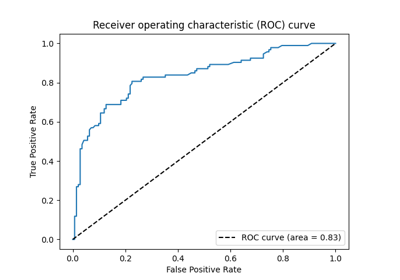
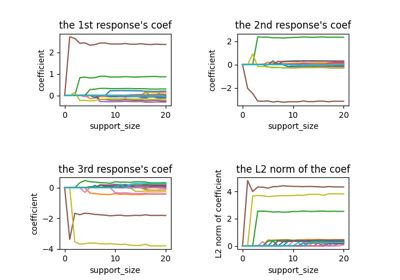
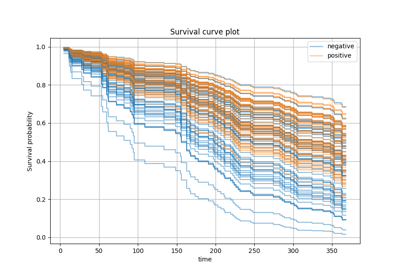
Tutorial#
The Tutorial section aims to provide working code samples demonstrating
how to use the abess library to solve real world issues.
In the following pages, the abess Python package is used for illustration.
The counterpart for R package is available at here.
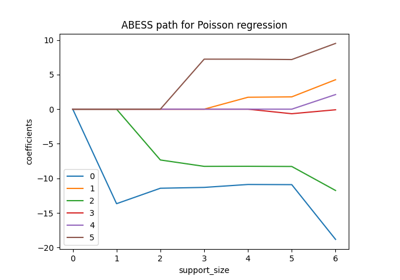
Generalized Linear Model#
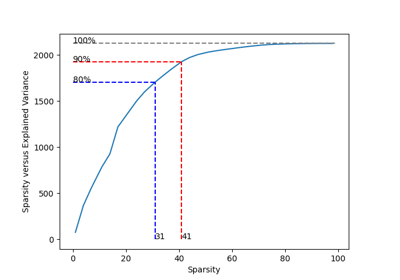
Principal Component Analysis#
Advanced Generic Features#
When analyzing the real world datasets, we may have the following targets:
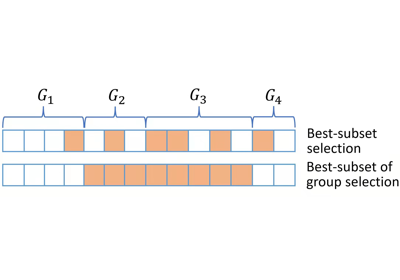
identifying predictors when group structure are provided (a.k.a., best group subset selection);
certain variables must be selected when some prior information is given (a.k.a., nuisance regression);
selecting the weak signal variables when the prediction performance is mainly interested (a.k.a., regularized best-subset selection).
These targets are frequently encountered in real world data analysis.
Actually, in our methods, the targets can be properly handled by simply change some default arguments in the functions.
In the following content, we will illustrate the statistic methods to reach these targets in a one-by-one manner,
and give quick examples to show how to perform the statistic methods in LinearRegression and
the same steps can be implemented in all methods.
Besides, abess library is very flexible, i.e., users can flexibly control many internal computational components.
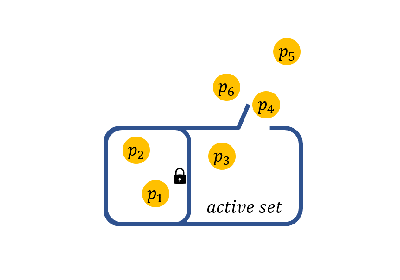
Specifically, users can specify: (i) the division of samples in cross validation (a.k.a., cross validation division),
(ii) specify the initial active set before splicing (a.k.a., initial active set), and so on.
We will also describe these in the following.
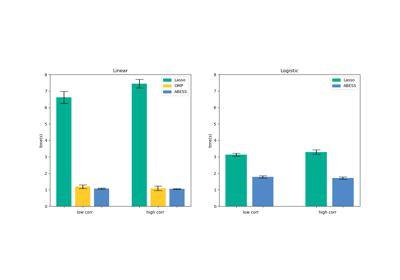
Computational Tips#
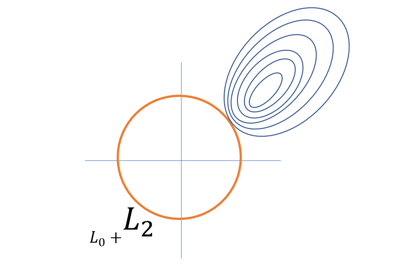
The generic splicing technique certifiably guarantees the best subset can be selected in a polynomial time. In practice, the computational efficiency can be improved to handle large scale datasets. The tips for computational improvement are applicable for:
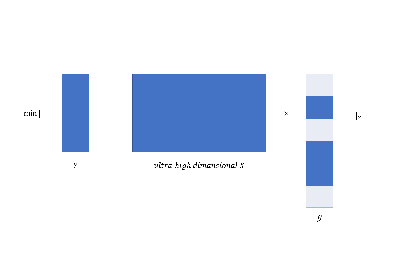
ultra-high dimensional data via
feature screening;
focus on important variables;
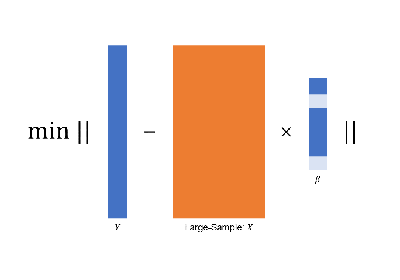
large-sample data via
golden-section searching;
early-stop scheme;
sparse inputs via
sparse matrix computation;
specific models via
covariance update for
LinearRegressionandMultiTaskRegression;quasi Newton iteration for
LogisticRegression,PoissonRegression,CoxRegression, etc.
More importantly, the technique in these tips can be use simultaneously.
For example, abess allow algorithms to use both feature screening and golden-section searching such that
algorithms can handle datasets with large-sample and ultra-high dimension.
The following contents illustrate the above tips.
Besides, abess efficiently implements warm-start initialization and parallel computing,
which are very useful for fast computing.
To help use leverage them, we will also describe their implementation details in the following.
Connect to Popular Libraries with scikit-learn API#
This part is intended to present all possible connection between abess and
other popular Python libraries via the scikit-learn interface.
It is keep developing and more examples will come up soon.
Contributions for this part is extremely welcome!