Note
Go to the end to download the full example code
Linear Regression#
In this tutorial, we are going to demonstrate how to use the abess package to carry out best subset selection
in linear regression with both simulated data and real data.
Our package abess implements a polynomial algorithm in the following best-subset selection problem:
where \(\| \cdot \|_2\) is the \(\ell_2\) norm, \(\|\beta\|_0=\sum_{i=1}^pI( \beta_i\neq 0)\)
is the \(\ell_0\) norm of \(\beta\), and the sparsity level \(s\)
is an unknown non-negative integer to be determined.
Next, we present an example to show the abess package can get an optimal estimation.
Toward optimality: adaptive best-subset selection#
Synthetic dataset#
We generate a design matrix \(X\) containing \(n = 300\) observations and each observation has \(p = 1000\) predictors. The response variable \(y\) is linearly related to the first, second, and fifth predictors in \(X\):
where \(\epsilon\) is a standard normal random variable.
import numpy as np
from abess.datasets import make_glm_data
np.random.seed(0)
n = 300
p = 1000
true_support_set=[0, 1, 4]
true_coef = np.array([3, 1.5, 2])
real_coef = np.zeros(p)
real_coef[true_support_set] = true_coef
data1 = make_glm_data(n=n, p=p, k=len(true_coef), family="gaussian", coef_=real_coef)
print(data1.x.shape)
print(data1.y.shape)
(300, 1000)
(300,)
This dataset is high-dimensional and brings large challenge for subset selection.
As a typical data examples, it mimics data appeared in real-world for modern scientific researches and data mining,
and serves a good quick example for demonstrating the power of the abess library.
Optimality#
The optimality of subset selection means:
true_support_set(i.e.[0, 1, 4]) can be exactly identified;the estimated coefficients is ordinary least squares (OLS) estimator under the true subset such that is very closed to
true_coef = np.array([3, 1.5, 2]).
To understand the second criterion, we take a look on the estimation given by scikit-learn library:
from sklearn.linear_model import LinearRegression as SKLLinearRegression
sklearn_lr = SKLLinearRegression()
sklearn_lr.fit(data1.x[:, [0, 1, 4]], data1.y)
print("OLS estimator: ", sklearn_lr.coef_)
OLS estimator: [3.00085183 1.44388323 2.00633204]
The fitted coefficients sklearn_lr.coef_ is OLS estimator
when the true support set is known.
It is very closed to the true_coef, and is hard to be improve under finite sample size.
Adaptive Best Subset Selection#
The adaptive best subset selection (ABESS) algorithm is a very powerful for the selection of the best subset. We will illustrate its power by showing it can reach to the optimality.
The following code shows the simple syntax for using ABESS algorithm via abess library.
from abess import LinearRegression
model = LinearRegression()
model.fit(data1.x, data1.y)
LinearRegression functions in abess is designed for selecting the best subset under the linear model,
which can be imported by: from abess import LinearRegression.
Following similar syntax like scikit-learn, we can fit the data via ABESS algorithm.
Next, we going to see that the above approach can successfully recover the true set np.array([0, 1, 4]).
The fitted coefficients are stored in model.coef_.
We use np.nonzero function to find the selected subset of abess,
and we can extract the non-zero entries in model.coef_ which is the coefficients estimation for the selected predictors.
ind = np.nonzero(model.coef_)
print("estimated non-zero: ", ind)
print("estimated coef: ", model.coef_[ind])
estimated non-zero: (array([0, 1, 4]),)
estimated coef: [3.00085183 1.44388323 2.00633204]
From the result, we know that abess exactly found the true set np.array([0, 1, 4]) among all 1000 predictors.
Besides, the estimated coefficients of them are quite close to the real ones,
and is exactly the same as the estimation sklearn_lr.coef_ given by scikit-learn.
Real data example#
Hitters Dataset#
Now we focus on real data on the Hitters dataset. We hope to use several predictors related to the performance of the baseball athletes last year to predict their salary.
First, let's have a look at this dataset. There are 19 variables except Salary and 322 observations.
import os
import pandas as pd
data2 = pd.read_csv(os.path.join(os.getcwd(), 'Hitters.csv'))
print(data2.shape)
print(data2.head(5))
(322, 20)
AtBat Hits HmRun Runs RBI ... PutOuts Assists Errors Salary NewLeague
0 293 66 1 30 29 ... 446 33 20 NaN A
1 315 81 7 24 38 ... 632 43 10 475.0 N
2 479 130 18 66 72 ... 880 82 14 480.0 A
3 496 141 20 65 78 ... 200 11 3 500.0 N
4 321 87 10 39 42 ... 805 40 4 91.5 N
[5 rows x 20 columns]
Since the dataset contains some missing values, we simply drop those rows with missing values. Then we have 263 observations remain:
data2 = data2.dropna()
print(data2.shape)
(263, 20)
What is more, before fitting, we need to transfer the character variables to dummy variables:
data2 = pd.get_dummies(data2)
data2 = data2.drop(['League_A', 'Division_E', 'NewLeague_A'], axis=1)
print(data2.shape)
print(data2.head(5))
(263, 20)
AtBat Hits HmRun Runs ... Salary League_N Division_W NewLeague_N
1 315 81 7 24 ... 475.0 True True True
2 479 130 18 66 ... 480.0 False True False
3 496 141 20 65 ... 500.0 True False True
4 321 87 10 39 ... 91.5 True False True
5 594 169 4 74 ... 750.0 False True False
[5 rows x 20 columns]
Model Fitting#
As what we do in simulated data, an adaptive best subset can be formed easily:
x = np.array(data2.drop('Salary', axis=1))
y = np.array(data2['Salary'])
model = LinearRegression(support_size=range(20))
model.fit(x, y)
The result can be shown as follows:
ind = np.nonzero(model.coef_)
print("non-zero:\n", data2.columns[ind])
print("coef:\n", model.coef_)
non-zero:
Index(['Hits', 'CRBI', 'PutOuts', 'League_N'], dtype='object')
coef:
[ 0. 2.67579779 0. 0. 0.
0. 0. 0. 0. 0.
0. 0.681779 0. 0.27350022 0.
0. 0. -139.9538855 0. ]
Automatically, variables Hits, CHits, CHmRun, PutOuts, League_N are chosen in the model (the chosen sparsity level is 5).
More on the results#
We can also plot the path of abess process:
import matplotlib.pyplot as plt
coef = np.zeros((20, 19))
ic = np.zeros(20)
for s in range(20):
model = LinearRegression(support_size=s)
model.fit(x, y)
coef[s, :] = model.coef_
ic[s] = model.eval_loss_
for i in range(19):
plt.plot(coef[:, i], label=i)
plt.xlabel('support_size')
plt.ylabel('coefficients')
plt.title('ABESS Path')
plt.show()
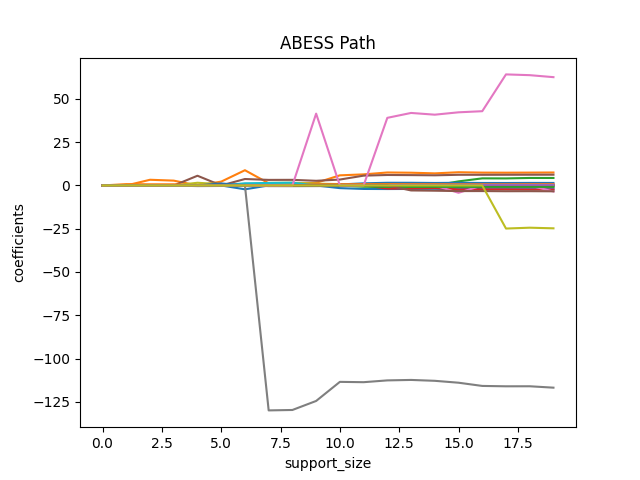
Besides, we can also generate a graph about the tuning parameter. Remember that we used the default EBIC to tune the support size.
plt.plot(ic, 'o-')
plt.xlabel('support_size')
plt.ylabel('EBIC')
plt.title('Model selection via EBIC')
plt.show()
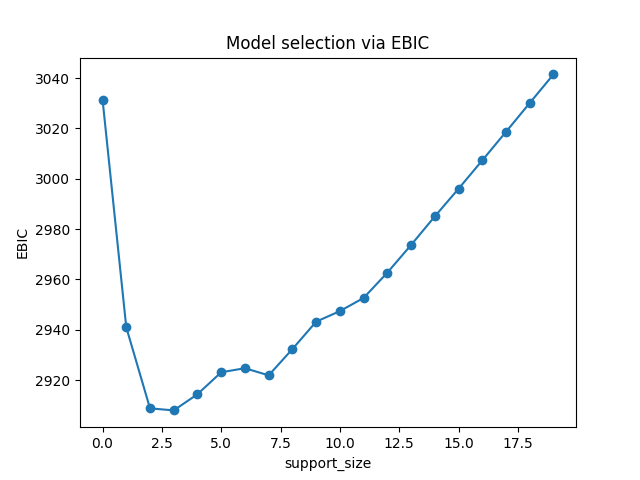
In EBIC criterion, a subset with the support size 4 has the lowest value, so the process adaptively chooses 4 variables. Note that under other information criteria, the result may be different.
R tutorial#
For R tutorial, please view https://abess-team.github.io/abess/articles/v01-abess-guide.html.
Total running time of the script: (0 minutes 1.797 seconds)