Note
Go to the end to download the full example code
Nuisance Regression#
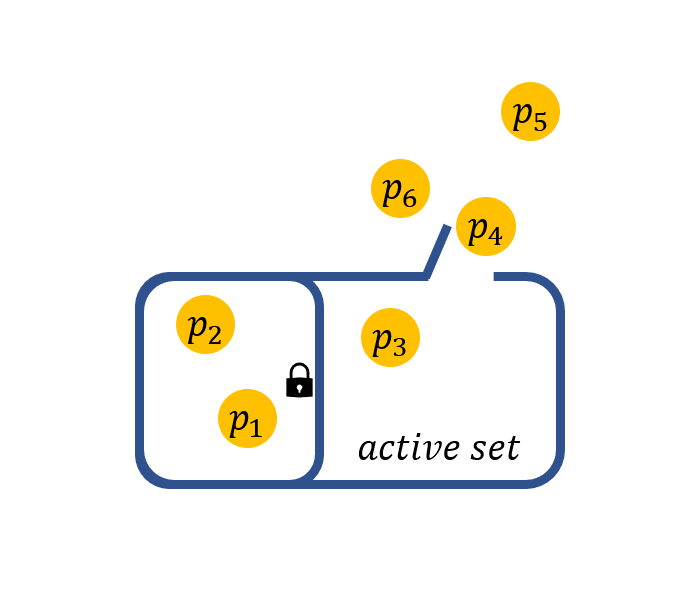
Introduction#
Nuisance regression refers to best subset selection with some prior information that some variables are required to stay in the active set. For example, if we are interested in a certain gene and want to find out what other genes are associated with the response when this particular gene shows effect. The nuisance selection can be achieved by solving:
Note that, the sparsity constraint restricts on \(\beta\) and not on \(\gamma\). The effect of \(\gamma\) corresponds to variables that stay in the active set.
Using: nuisance regression#
In the LinearRegression() (or other methods), the argument always_select is designed to realize this goal.
Users can pass a list containing the indexes of the target variables to
always_select.
Here is an example demonstrating the advantage of nuisance selection. We generate a high-dimensional dataset whose predictors are highly correlated (pairwise correlation: 0.6) and the effect of predictors on response is weaker than noise.
import numpy as np
from abess.datasets import make_glm_data
# generate dataset
np.random.seed(12345)
data = make_glm_data(n=100, p=500, k=3, rho=0.6, family='gaussian', snr=0.5)
print('True effective subset: ', np.nonzero(data.coef_))
True effective subset: (array([ 87, 271, 449]),)
We use the standard abess to tackle this dataset:
from abess.linear import LinearRegression
model = LinearRegression(support_size=range(10))
model.fit(data.x, data.y)
print('Estimated subset:', np.nonzero(model.coef_))
Estimated subset: (array([271, 449]),)
The result from model omits the 87-th predictor belonging to the true effective set.
But if we suppose that the 87-th predictor are worthy to be
included in the model, we can call:
model = LinearRegression(support_size=range(10), always_select=[87])
model.fit(data.x, data.y)
print('Estimated subset:', np.nonzero(model.coef_))
Estimated subset: (array([ 87, 400, 449]),)
Now the estimated subset is the same as the true effective set. The comparison between nuisance selection and standard ABESS suggests that reasonably leveraging prior information promotes the quality of subset selection.
The abess R package also supports nuisance regression.
For R tutorial, please view
https://abess-team.github.io/abess/articles/v07-advancedFeatures.html.
sphinx_gallery_thumbnail_path = 'Tutorial/figure/nuisance_cover.png'
Total running time of the script: (0 minutes 0.094 seconds)