Note
Go to the end to download the full example code
Large-Sample Data#
Introduction#
A large sample size leads to a large range of possible support sizes which adds to the computational burdon. The computational tip here is to use the golden-section searching to avoid support size enumeration.
A motivated observation#
Here we generate a simple example under linear model via make_glm_data.
from time import time
import numpy as np
import matplotlib.pyplot as plt
from abess.datasets import make_glm_data
from abess.linear import LinearRegression
np.random.seed(0)
data = make_glm_data(n=100, p=20, k=5, family='gaussian')
ic = np.zeros(21)
for sz in range(21):
model = LinearRegression(support_size=[sz], ic_type='ebic')
model.fit(data.x, data.y)
ic[sz] = model.eval_loss_
print("lowest point: ", np.argmin(ic))
lowest point: 5
The generated data contains 100 observations with 20 predictors,
while 5 of them are useful (has non-zero coefficients).
Uses extended Bayesian information criterion (EBIC), the abess successfully detect the true support size.
We go further and take a look on the support size versus EBIC returned
by LinearRegression in abess.linear.
plt.plot(ic, 'o-')
plt.xlabel('support size')
plt.ylabel('EBIC')
plt.title('Model Selection via EBIC')
plt.show()
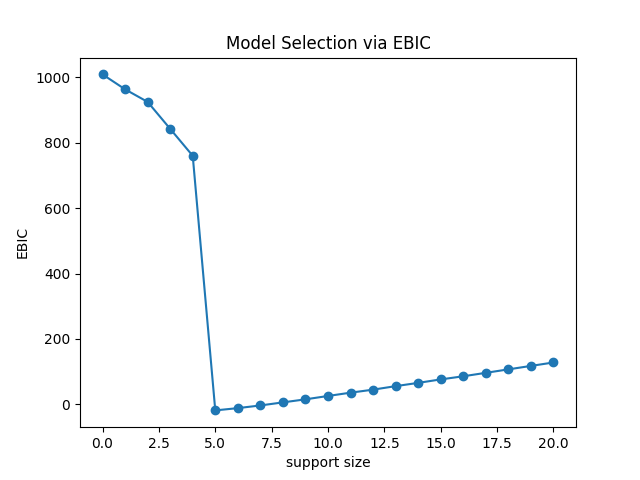
From the figure, we can find that
the curve should is a strictly unimodal function achieving minimum at the true subset size,
where support_size = 5 is the lowest point.
Motivated by this observation, we consider a golden-section search technique to determine the optimal support size associated with the minimum EBIC.
Compare to the sequential searching, the golden section is much faster because it skip some support sizes which are likely to be a non-optimal one. Precisely, searching the optimal support size one by one from a candidate set with \(O(s_{max})\) complexity, golden-section reduce the time complexity to \(O(\ln(s_{max}))\), giving a significant computational improvement.
Usage: golden-section#
In abess package, golden-section technique can be easily formed like:
model = LinearRegression(path_type='gs', s_min=0, s_max=20)
model.fit(data.x, data.y)
print("real coef:\n", np.nonzero(data.coef_)[0])
print("predicted coef:\n", np.nonzero(model.coef_)[0])
real coef:
[ 2 5 10 11 18]
predicted coef:
[ 2 5 10 11 18]
where path_type = 'gs' means using golden-section rather than search the support size one-by-one.
s_min and s_max indicates the left and right bound of range of the support size.
Note that in golden-section searching, we should not give support_size, which is only useful for sequential strategy.
The output of golden-section strategy suggests the optimal model size is accurately detected.
Golden-section v.s. Sequential-searching: runtime comparison#
In this part, we perform a runtime comparison experiment to demonstrate the speed gain brought by golden-section.
sequential time: 0.0019352436065673828
golden-section time: 0.0011239051818847656
The golden-section runs much faster than sequential method. The speed gain would be enlarged when the range of support size is larger.
The abess R package also supports golden-section.
For R tutorial, please view
https://abess-team.github.io/abess/articles/v09-fasterSetting.html.
sphinx_gallery_thumbnail_path = 'Tutorial/figure/large-sample.png'
Total running time of the script: (0 minutes 0.147 seconds)