Best Subset of Group Selection

Introduction

Best subset of group selection (BSGS) aims to choose a small part of non-overlapping groups to achieve the best interpretability on the response variable. BSGS is practically useful for the analysis of ubiquitously existing variables with certain group structures. For instance, a categorical variable with several levels is often represented by a group of dummy variables. Besides, in a nonparametric additive model, a continuous component can be represented by a set of basis functions (e.g., a linear combination of spline basis functions). Finally, specific prior knowledge can impose group structures on variables. A typical example is that the genes belonging to the same biological pathway can be considered as a group in the genomic data analysis. Figure for distinct BSGS and best-subset selection is presented below.

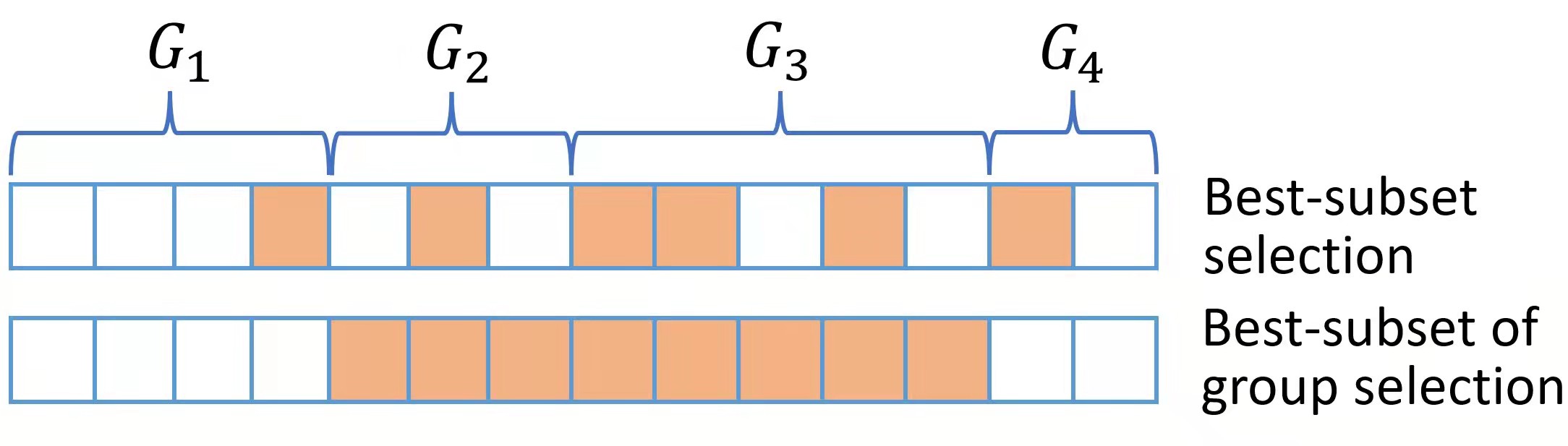
The BSGS can be achieved by solving:

\[\min_{\beta\in \mathbb{R}^p} \frac{1}{2n} ||y-X\beta||_2^2,\; \textup{s.t.}\ ||\beta||_{0,2}\leq s .\]

where \(||\beta||_{0,2} = \sum_{j=1}^J I(||\beta_{G_j}||_2\neq 0)\) in which \(||\cdot||_2\) is the \(\ell_2\) norm and model size \(s\) is a positive integer to be determined from data.

Regardless of the NP-hard of this problem, Zhang et al develop a certifiably polynomial algorithm to solve it. This algorithm is integrated in the abess package, and user can handily select best group subset by assigning a proper value to the group arguments:

Using best group subset selection

We still use the dataset data generated before, which has 100 samples, 5 useful variables and 15 irrelevant variables.

import numpy as np
from abess.datasets import make_glm_data
from abess.linear import LinearRegression

np.random.seed(0)

# generate data
n = 100
p = 20
k = 5
coef1 = 0.5*np.ones(5)
coef2 = np.zeros(5)
coef3 = 0.5*np.ones(5)
coef4 = np.zeros(5)
coef = np.hstack((coef1, coef2, coef3, coef4))
data = make_glm_data(n=n, p=p, k=k, family='gaussian', coef_ = coef)
print('real coefficients:\n', data.coef_, '\n')

real coefficients:
 [0.5 0.5 0.5 0.5 0.5 0.  0.  0.  0.  0.  0.5 0.5 0.5 0.5 0.5 0.  0.  0.
 0.  0. ]

Support we have some prior information that every 5 variables as a group:

group = np.linspace(0, 3, 4).repeat(5)
print('group index:\n', group)

group index:
 [0. 0. 0. 0. 0. 1. 1. 1. 1. 1. 2. 2. 2. 2. 2. 3. 3. 3. 3. 3.]

Then we can set the group argument in function. Besides, the support_size here indicates the number of groups, instead of the number of variables. Similarly, always_select, A_init and other parameters related to "index" should also be group index, instead of the variable one.

model1 = LinearRegression(support_size=range(3), group=group)
model1.fit(data.x, data.y)
print('coefficients:\n', model1.coef_)

coefficients:
 [0.65915697 0.45713643 0.49044526 0.43927599 0.62863533 0.
 0.         0.         0.         0.         0.575272   0.41249505
 0.37598688 0.59901008 0.58798189 0.         0.         0.
 0.         0.        ]

The fitted result suggest that only two groups are selected (since support_size is from 0 to 2) and the selected variables are shown above.

Next, we want to compare the result of a given group structure with that without a given group structure.

model2 = LinearRegression()
model2.fit(data.x, data.y)
print('coefficients:\n', model2.coef_)

coefficients:
 [0.61823344 0.54500673 0.59272352 0.42754021 0.65843857 0.
 0.         0.         0.         0.         0.         0.
 0.         0.66978731 0.55137187 0.         0.         0.
 0.         0.        ]

The result from a model without a given group structure omits three predictors belonging to the active set. The abess R package also supports best group subset selection.

For R tutorial, please view https://abess-team.github.io/abess/articles/v07-advancedFeatures.html.

sphinx_gallery_thumbnail_path = 'Tutorial/figure/best-subset-group-selection.png'